Find All Points (X Y) on the Curve Where the Line Tangent

Agile Overview

• To find the equation of a line you demand a point and a slope.
• The pitch of the tangent line is the apprais of the differential at the point of tangency.
• The normal telephone line is a line that is perpendicular to the tangent line and passes through the point of tangency.

Examples

Example 1

Suppose $$f(x) = x^3$$. Find the equation of the tangent line at the point where $$x = 2$$.

Step 1

Find the orient of tangency.

Since $$x=2$$, we evaluate $$f(2)$$.

$$ f(2) = 2^3 = 8 $$

The point is $$(2,8)$$.

Pace 2

Find the value of the derivative at $$x = 2$$.

$$ f'(x) = 3x^2\longrightarrow f'(2) = 3(2^2) = 12 $$

The the slope of the tangent line is $$m = 12$$.

Step 3

Find the point-slope phase of the line with slope $$m = 12$$ through the taper off $$(2,8)$$.

$$ \begin{adjust*} y - y_1 & = m(x-x_1)\\[6pt] y - 8 & = 12(x-2) \end{align*} $$

Answer

$$y - 8 = 12(x-2)$$

For reference, here is the graph of the function and the tangent line we just found.

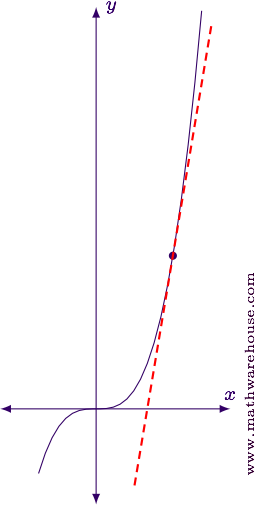
Exemplar 2

Suppose $$f(x) = x^2 - x$$. Find the equation of the tangent line with slope $$m = -3$$.

Step 1

Find the derivative.

$$ f'(x) = 2x -1 $$

Step 2

Find the $$x$$-value where $$f'(x)$$ equals the slope.

$$ \begin{align*} f'(x) & = 2x -1\\[6pt] -3 &adenylic acid; = 2x -1\\[6pt] -2 & = 2x\\[6pt] x & = -1 \death{adjust*} $$

Step 3

Find the point on the function where $$x = -1$$.

$$ f(-1) = (-1)^2 - (-1) = 1 + 1 = 2 $$

The signal is $$(-1, 2)$$.

Tread 4

Find the equation of the line through the point $$(-1,2)$$ with slope $$m=-3$$.

$$ \lead off{align*} y -y_1 & = m(x-x_1)\\[6pt] y - 2 & = -3(x - (-1))\\[6pt] y - 2 & = -3(x+1) \end{align*} $$

Answer

$$ y - 2 = -3(x+1) $$

For reference, here's the graphical record of the role and the tangent line we just found.

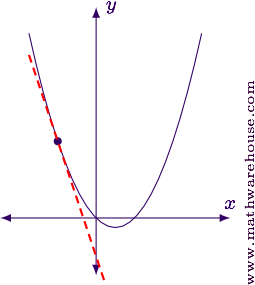
Tangent Lines to Implicit Curves

The procedure doesn't change when working with implicitly outlined curves.

Example 3

Guess $$x^2 + y^2 = 16$$. Chance the equation of the tan draw at $$x = 2$$ for $$y>0$$.

Step out 1

Find the $$y$$-value of the point of tangency.

$$ \begin{align*} \blue{x^2} + y^2 & = 16\\[6pt] \chromatic{2^2} + y^2 & = 16\\[6pt] \blueness{4} + y^2 & = 16\\[6pt] y^2 & = 12\\[6pt] y & = \pm\sqrt{12}\\[6pt] y & = \pm\sqrt{4\cdot 3}\\[6pt] y &ere; = \pm2\sqrt 3 \end{ordinate*} $$

Since the problem states we are interested in $$y>0$$, we use $$y = 2\sqrt 3$$.

The point of tangency is $$(2, 2\sqrt 3)$$.

Step 2

Find the equation for $$\frac{dy}{dx}$$.

Since the equation is implicitly defined, we expend implicit differentiation.

$$ \begin{ordinate*} 2x + 2y\,\frac{dy}{dx} & = 0\\[6pt] 2y\,\frac{dy}{dx} & = -2x\\[6pt] \frac{dy}{dx} & = -\frac{2x}{2y}\\[6pt] \frac{Dy}{dx} &A; = -\frac x y \end{align*} $$

Step 3

Line up the slope of the tangent line at the point of contact.

At the target $$(2,2\sqrt 3)$$, the slope of the tan line is

$$ \set about{array*} \frac{dy}{dx}\bigg|_{(\depressing{2},\red{2\sqrt 3})} & = -\frac {\blue 2} {\flushed{2\sqrt 3}}\\[6pt] & = -\frac 1 {\sqrt 3}\\[6pt] & = -\frac 1 {\sqrt 3}\cdot \blue{\frac{\sqrt 3}{\sqrt 3}}\\[6pt] & = -\frac{\sqrt 3} 3 \end{align*} $$

The slope of the tangent crinkle is $$m = -\frac{\sqrt 3} 3$$.

Whole step 4

Find the equation of the tangent stoc through $$(2,2\sqrt 3)$$ with a slope of $$m=-\frac{\sqrt 3} 3$$.

At the point $$(2,2\sqrt 3)$$, the pitch of the tangent dividing line is

$$ \begin{align*} y - y_1 & = m(x-x_1)\\[6pt] y - 2\sqrt 3 & = -\frac{\sqrt 3} 3(x-2) \end{align*} $$

Result

The equation of the tan line is $$y - 2\sqrt 3 = -\frac{\sqrt 3} 3(x-2)$$

For credit, the graph of the curve and the tan line we found is shown down the stairs.

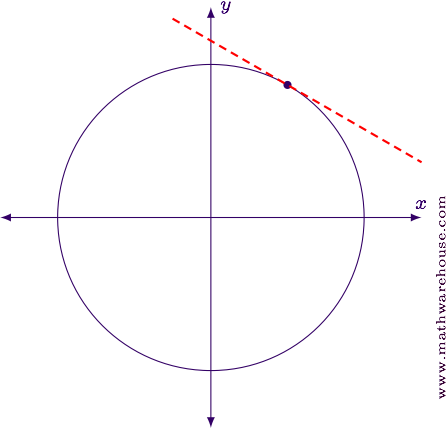
Normal Lines

Hypothecate we have a a tangent line to a function. The function and the tangent line intersect at the point of tangency. The line through that same point that is perpendicular to the tangent line is known as a sane line.

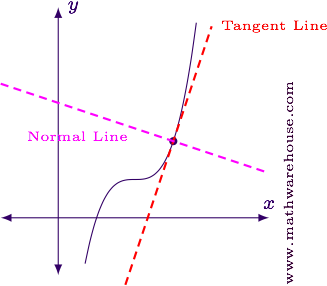
Recall that when two lines are perpendicular, their slopes are negative reciprocals. Since the pitch of the tangent line is $$m = f'(x)$$, the incline of the sane line of business is $$m = -\frac 1 {f'(x)}$$.

Example 4

Suppose $$f(x) = \romaine x$$. Find the par of the cable that is normal to the function at $$x = \frac \pi 6$$.

Dance step 1

Find the stop on the function.

$$ f\left(\frac \PI 6\right) = \romaine \frac \pi 6 = \frac{\sqrt 3} 2 $$

The place is $$\left(\frac \sherloc 6, \frac{\sqrt 3} 2\decent)$$.

Step 2

Find the value of the derivative at $$x = \frac \pi 6$$.

$$ f'(x) = -\sin x\longrightarrow f'\left(\frac \pi 6\right) = -\sin\frac\PI 6 = -\frac 1 2 $$

The incline of the tangent line is $$m = -\frac 1 2$$. Since we are looking for the pedigree that is perpendicular to the tangent melody, we want to use $$m = 2$$.

Stone's throw 3

See the equation of the line through the maneuver $$\left(\frac \private investigator 6, \frac{\sqrt 3} 2\right)$$ with a slope of $$m =2$$.

$$ \begin{align*} y -y_1 & = m(x-x_1)\\[6pt] y - \frac{\sqrt 3} 2 &ere; = 2\left(x - \frac \private eye 6\right) \end{aline*} $$

Respond

The wrinkle normal to the function at $$x = \frac \pi 6$$ is $$y - \frac{\sqrt 3} 2 = 2\port(x - \frac \pi 6\right)$$.

For reference, here is the chart of the function and the normal line we found.

Continue to Practice Problems

Fault : Please Click on "Not a robot", then try downloading again.

Find All Points (X Y) on the Curve Where the Line Tangent

Source: https://www.mathwarehouse.com/calculus/derivatives/how-to-find-equations-of-tangent-lines.php

Bagikan Artikel ini